Break Even Point und das Gesetz der Massenproduktion
Der Break Even Point ist der Punkt, ab dem ein Produktionsverfahren einen Nutzen erzielt.
Mit Nutzen ist in der Betriebswirtschaft der allgemeine Gewinn gemeint.
Ganz konkret gesagt…
Ab dem Break Even Point machst du Gewinn in deinem Unternehmen.
Alles was vorher war, ist das reine Verlustgeschäft.
Da dieser Punkt einen Wendepunkt darstellt, nennt man den Break Even Point auch Nutzenschwelle oder Gewinnschwelle.
Doch schauen wir uns den Punkt einmal an.
Inhalt
Break Even Point an ein paar Beispielen
Bevor wir anfangen, noch ein paar Begrifflichkeiten…
Denn du solltest diese kennen und auch verstehen, bevor du den BEP (Break Even Point) berechnen kannst.
Fixe Kosten sind die entscheidende Komponenten beim Break Even Point
Fixe Kosten sind alle Kosten, welche egal wie viel du produzierst – immer gleich bleiben.
Zum Beispiel bist du ein Transportunternehmer mit LKW’s.
Dann schaffst du dir einen LKW an.
Dieser kostet Summe „x“ in der Anschaffung.
Egal, wie weit du mit dem LKW fährst, die Anschaffungskosten werden weder steigen noch fallen.
Diese sind immer fix, also fest.
Ein anderes Beispiel wäre in einem Restaurant.
Du kaufst dir einen neuen Superherd.
Ganz egal, wie viel du mit dem Teil kochst – die gesamten Anschaffungskosten bleiben die gleichen.
Weitere Beispiele für feste bzw. fixe Kosten wären feste Löhne ohne Zuschläge, Anschaffungskosten für Computer oder Schreibtische.
Aber auch im privaten Bereich, wäre eine Handy-Flatrate mit All-in Service – fixe monatliche Kosten.
Aber jetzt kommt’s.
Fixe Kosten lassen sich in der Menge verteilen.
Denn, wenn du die fixen Stückkosten berechnest – verändern sich zwar die Gesamtkosten nach wie vor nicht, aber die Stückkosten je Einheit verändern sich schon.
Fixe Kostenverteilung im 1. Beispiel
Beginnen wir beim LKW.
Dieser kostet 80.000 Euro in der Anschaffung.
Es ist völlig egal, ob du damit nur 100 km im Jahr fährst oder 10.000 km im Jahr – die gesamten Anschaffungskosten bleiben gleich.
Fixe Gesamtkosten eben.
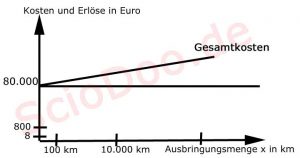
Wie hier im Bild zu sehen ist.
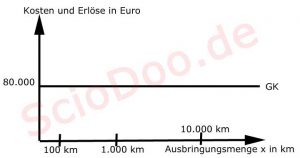
Was siehst du?
- Auf der y Achse sind die Kosten bereits eingetragen. Später werden noch die Umsätze abgetragen.
- Und die x Achse zeigt die Ausbringungsmenge x. In diesem Fall sind das die gefahrenen Kilometer
- Die schwarze Linie, welche parallel zur x-Achse verläuft, zeigt die fixen Gesamtkosten (GK).
- Da die GK von 80.000 Euro bei 100, 1000 oder 10.000 und selbst bei einer Million km immer gleich sind – verläuft diese Linie waagerecht bei 80.000 Euro.
Aber im Produktionsmodell spielen die fixen Stückkosten, die alles entscheidende Rolle.
Denn wenn du:
- 100 km fährst – kostet ein Kilometer 80.000/100=800 Euro.
- Bei 10.000 km kostet ein Kilometer nur 80.000/10.000 = 8 Euro.
Die Gesamtkosten sind nach wie vor unverändert.
Jedoch die Stückkosten fallen mit zunehmender Ausbringungsmenge.
Das ist die Massenproduktionstheorie.
So wie hier im Bild.
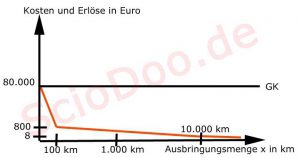
- Bei 0 km sind die Stückkosten natürlich noch bei 80.000 Euro.
- Und bei einem Kilometer sind diese ebenfalls so hoch, denn 80.000/1=80.000.
- Aber schon beim zweiten Kilometer halbieren sich die fixen Stückkosten (80.000/2)
- Bei 100 km liegen diese bei 800 Euro und bei 10.000 km nur noch bei 8 Euro.
Cool, oder?
Beispiel 2 zu den fixen Kosten
Schauen wir uns das Restaurant mit dem Herd einmal an.
Der Herd kostet vielleicht 10.000 Euro.
Egal, wie viel Essen du zubereitest – die gesamten Fixkosten bleiben gleich.
Aber es macht einen Unterschied bei den Stückkosten, ob du 10 Essen im Jahr zubereitest oder 10.000.
Denn auch hier gilt das Prinzip der fallenden fixen Stückkosten.
- Bei 100 Mahlzeiten würden die fixen Stückkosten 10.000/100=100 Euro betragen
- Und bei 10.000 Mahlzeiten wären die fixen Stückkosten auf 1 Euro pro Mahlzeit gefallen.
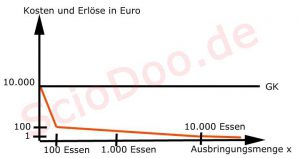
Beispiel 3 zu fallenden Fixkosten
Was in der Betriebswirtschaft gilt, gilt auch im privaten Sektor.
Deine Handy Flatrate kostet 20 Euro monatlich, egal ob du damit 100 Minuten oder 10 Minuten telefoniert hast.
Wenn du allerdings 100 Minuten telefoniert hast, kostet dich die Gesprächsminute 20/100=0,2 Euro.
Bei 10 Minuten im Monat fallen die Gesprächskosten pro Minute deutlich höher aus: 20/10=2 Euro.
Sicherlich ist dies bei einer Flatrate kaum interessant.
Aber vielleicht willst du wissen, ob sich die Flat überhaupt lohnt.
Oder ab wie viel Minuten eine Flatrate günstiger ist, gegenüber dem Tarifmodell.
All das kannst du mit der Break Even Analyse bestimmen.
Fazit zu den fallenden fixen Stückkosten
Dies war eigentlich schon der Hebel, der Lehrsatz bzw. das ganze Prinzip zum Break Even Point.
Fixe Kosten fallen mit zunehmender Ausbringungsmenge.
Doch es gibt noch ein paar andere Kostenarten, welche herangezogen werden müssen – um den Break-Even-Point berechnen zu können.
Variable Gesamtkosten steigen mit der Ausbringungsmenge
Beginnen wir beim LKW.
Variable Kosten sind zum Beispiel der Sprit bzw. das Benzin.
Wenn der LKW 80.000 Euro in der Anschaffung und das Benzin 0,25 Euro pro Kilometer kostet – ergeben sich folgende Kostenfunktionen bei 100 und 10.000 km:
- 80.000 + 100 * 0,25 = 80.025 Euro Gesamtkosten bei 100 km.
Stückkosten belaufen sich dann auf 80.025/100=800,25 Euro je Kilometer. - Bei 10.000 km betragen die Gesamtkosten 80.000 + 10.000 * 0,25=82.500 Euro.
Diese sind aufgrund der Kilometerleistung und den damit verbundenen Kilometersatz etwas höher.
Aber ein Blick auf die Stückkosten verrät, dass diese deutlich niedriger ausfallen.
82.500/10.000=8,25 Euro je Kilometer
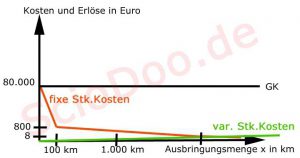
Wenn du dir die variablen Stückkosten einmal anschaust, siehst du – diese beginnen bei Null.
Dies ist ganz logisch, denn – wenn der LKW nicht bzw. 0 km fährt, fallen auch keine Spritkosten an.
Die variablen Benzin- bzw. Spritkosten steigen pro Kilometer um den Wert 0,25 Euro.
Dadurch, dass der Anstieg gleichbleibend ist – nennt man dies auch einen linearen Kostenverlauf.
Beim Restaurant Beispiel könnten die variablen Kosten – der Strom sein oder Zutaten.
Variable Kosten beim Handy könnte ebenfalls der Strom sein.
Ich mache es mir einfach…
Denn ich unterstelle einfach einmal, dass eine Mahlzeit 2 Euro variable Kosten verursacht.
Und eine Einheit Strom beim Handy 0,15 Euro kostet.
Weitere Kosten beim Break Even Point
Alle drei Beispiele sind stark vereinfacht, denn zum LKW gehören auch Schmiermittel oder Versicherungen.
Natürlich gehören zum Produktionsprozess auch der Fahrer und sein Gehalt dazu.
Weiterhin sind variable Kosten, wie Spesen möglich.
Und genauso gut fallen dir wahrscheinlich noch andere Kosten beim Handy oder Herd ein.
Ich möchte das Beispiel allerdings so einfach, wie möglich halten.
Hier geht es nicht primär darum, dir eine genaue Kalkulation zu liefern.
Stattdessen möchte ich, dass du das Prinzip verstehst und es selbst anwenden kannst.
Also machen wir weiter im Text.
So kannst du den Break Even Point berechnen
Wir haben bisher die Kostenfunktionen für alle drei Beispiele:
- Gesamtkosten = Fixe Gesamtkosten + Variable Gesamtkosten
- Oder Gesamtkosten = fixe Gesamtkosten + variable Stückkosten multipliziert mit der Ausbringungsmenge
Die Ausbringungsmenge wäre die Anzahl der Mahlzeiten, die Gesprächsminuten oder die Fahrkilometer.
Diese Menge wird allgemein mit „x“ bezeichnet.
Hier die Funktionen:
- LKW: Gesamtkosten = 80.000 + 0,25 Euro * x
- Herd: Gesamtkosten = 10.000 + 2 Euro * x
- Handy: Gesamtkosten = 20 + 0,15 Euro * x
Die variablen Stückkosten + gesamten Fixkosten ergeben dann die Gesamtkosten.
Okay, wir wollen den Break – Even – Point berechnen.
Das ist der Punkt, an dem die Produktionsprozesse erstmalig Gewinne erwirtschaften.
Die Kosten haben wir. Aber zum Gewinn, brauchen wir noch Umsätze.
Denn Umsatz – Kosten = Gewinn.
Wie könnten die Umsatzfunktionen aussehen?
Nehmen wir einmal an, dass der LKW einen Kilometersatz für die transportierende Ware erhält.
Der Kunde des Transportunternehmens bzw. des Spediteurs könnte vielleicht 1,2 Euro pro gefahrenen Kilometer zahlen.
- Kostenfunktion: = 80.000 +0,25 Euro * x
- Umsatzfunktion: = 1,20 * x
Die Ausbringungsmenge x ist in diesem Fall der Kilometersatz.
Der Kunde zahlt pro Kilometer (Umsatzfunktion) und die gesamten variablen Kosten steigen pro Kilometer (Benzin).
Deshalb taucht die gleiche Variable x in beiden Funktionen auf.
Beim Break Even Point sind Kosten und Umsatz gleich groß.
Also müssen beide Funktionen gleichgesetzt und dann nach x umgestellt werden.
- Gleichsetzen: 80.000+0,25*x = 1,20*x
- Umstellen: 80.000+0,25x =1,20x |-0,25x – dadurch gelangt der Term auf die andere Seite (Matheregel)
- 80.000 = 1,20x – 0,25x | x und x zusammenziehen
- 80.000= 0,95x | durch 0,95
- 80.000/0,95 = 84.210,53
Okay, ab dem 84.211 Kilometer macht das Fahrzeug Gewinn.
Ich hoffe nur, dass ich mich nicht verrechnet habe.
Aber ich kann es überprüfen.
Dazu muss ich nur die 84.210,53 Kilometer in die Kosten- und Umsatzfunktion einsetzen.
Denn ich schrieb bereits, dass beim Break Even Point – Umsatz und Kosten gleich groß sind.
- Kosten: 80.000 + 0,25 * 84.210,53 = 101.052,63 Euro
- Umsatz: 1,20 * 84.210,53 = 101.052,63 Euro
Und passt, oder?
Interpretieren wir einmal das Ergebnis.
Vom 1 Kilometer an bis zum 84.209 Kilometer hat der LKW, mit dieser Kosten- und Preisstruktur – nur Minus gemacht.
Beim 84.210. Kilometer waren Kosten und Umsatz gleich groß.
Ab dem 84.211. Kilometer ist jeder weitere Kilometer in der Gewinnzone.
Hier die Grafik…
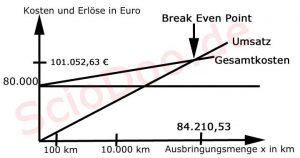
Ich weiß meine Grafik ist nach mathematischer Ordnung nicht einwandfrei.
Aber ich glaube, du erkennst trotzdem um was es geht.
- Links auf der y-Achse habe ich den Break Even Umsatz eingetragen.
Dieser liegt bei 101.052,63 Euro - Unten, auf der x-Achse, ist die kritische Ausbringungsmenge.
Diese liegt bei 84.210,53 km. - Außerdem ist die Umsatzfunktion Umsatz=1,2x und die Gesamtkostenkostenfunktion GK=80.000+0,25x eingetragen.
- Der Schnittpunkt zwischen Umsatzfunktion und Gesamtkostenfunktion ist der Break Even Point
Was besagt das Gesetz der Massenproduktion
Die gesamten Stückkosten sinken mit zunehmender Ausbringungsmenge.
Der Grund dafür sind die sinkenden fixen Kosten je Stück.
Umso mehr produziert wird, umso günstiger wird die Produktion.
Zusammenfassung:
- Der Break Even Point ist der Punkt, an dem die Gesamtkosten und der Gesamtumsatz gleich sind.
- Den Break Even Point kannst du entweder mathematisch durch Gleichsetzen oder grafisch durch Einzeichnen bestimmen.
- Der Break Even Umsatz ist der Umsatz, welcher an der Nutzenschwelle (Break Even Point) erzielt wurde.
- Ab der Nutzenschwelle fährt jede zusätzlich produzierte Einheit Gewinne ein.
- Hier liegt die Gewinnschwelle bzw. der Punkt – wo aus Minus, Plus wird
Über den Autor
