Rechenweg, um Binäre Zahlen in Dezimalzahlen umzuwandeln

Man verwendet oft die Zahlen 0 und 1.
Es können aber auch sämtliche anderen Zahlenpaare sein.
Zum Beispiel 7 und 175 sind für sich genommen, auch ein normales Zahlenpaar und somit ein Dualsystem.

Mit Null und Eins lässt sich aber am Leichtesten umrechnen.
Und daher bilden diese beiden Zahlen einen Standard im Dualsystem.

Wozu brauchst du das Binäre Zahlensystem?

Du benötigst dieses Zahlensystem in der Informatik und Elektronik.
Denn damit lassen sich die Zustände „AN“ und „AUS“ sehr leicht erzeugen.
Aber auch andere Zustände, wie „wahr“ oder „falsch“ lassen sich darstellen.

Diese beiden Zahlen können entsprechend unserem „normalen“ Dezimalsystem verwendet werden.
Du kannst sie addieren, subtrahieren, multiplizieren und dividieren.

Und weil dieses Zahlensystem speziell in der Informatik verwendet wird, haben sich auch entsprechende Größeneinheiten herausgebildet, wie:

• Bit
• Byte
• Kilobyte
• Terrabyte

In diesem Beitrag zeige ich dir die Grundlagen zum Dualsystem.
Du wirst lernen, wie du eine binäre Zahl in eine Dezimalzahl umwandelst.
Und du erfährst von mir, wie sich die Maßeinheiten in der Informatik berechnen lassen.

Der Unterschied zwischen dem Dualen Zahlensystem und dem Dezimalen Zahlensystem

Unser normales Zahlensystem heißt Dezimalsystem.
Die mathematische Grundlage dieses System umfasst 10 Ziffern.
Und zwar die Ziffern 0 bis 9.

Mittels Kombination dieser 10 Ziffern lassen sich alle Dezimalzahlen darstellen.
Zum Beispiel ist die Zahl 653 eine Kombination aus den Ziffern 6, 5 und 3.

Aber nicht nur das.
Denn alle Zahlen im Dezimalsystem bestehen aus 10-Potenzen.

• 6 * 10 hoch 2
• 5 * 10 hoch 1
• 3 * 10 hoch 0.

Halten wir fest.
Zehn Ziffern und somit ist jede Zahl, als 10-Potenz darstellbar.

Wenn du jetzt die dualen Zahlen einmal anschaust, bestehen diese lediglich aus zwei Ziffern.
Meistens sind es die 0 und die 1.

Und wenn dieses Binärsystem den selben Regeln folgt, wie das Dezimalsystem – dann müssten sich alle Zahlen als zweier Potenz darstellen lassen.
Und so ist es auch.

Die Umrechnung einer Binärzahl in eine Dezimalzahl

Beginnen wir mit einer kleinen und leichten Zahl.
Der binären Zahl 101.

Welche dezimale Zahl verbirgt sich hinter der binären Zahl 101?
Wäre die Zahl 101 dezimal, würden wir diese als 10-Potenz darstellen und die Summe ermitteln.

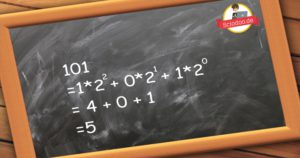
• 1 mal 2 hoch 2 = 4
• 0 * 2 hoch 1 = 0
• 1 * 2 hoch 0 = 1

Und die Summe ist dann Fünf.
Denn 4 + 0 + 1 =5
Die binäre Zahl 101 entspricht somit in einer Dezimalschreibweise der Zahl 5.

Zweites Beispiel ist etwas schwieriger und länger.
Die binäre Zahl 100010111.

Für einen besseren Überblick, bietet es sich an, von hinten anzufangen.
Du beginnst also nicht mit der höchsten Potenz – sondern mit der niedrigsten.
Dies hat den Vorteil, dass du mit der Null-Potenz beginnst und dann hochzählst.

Beginnen wir also von hinten.
Die letzte Ziffer ist die 1.
Somit wäre dies dann 1 * 2 hoch 0. Und dies wäre 1.

Hier die komplette Umrechnung:

• 1 * 2 hoch 0 = 1
• 1 * 2 hoch 1 = 1
• 1 * 2 hoch 2 = 4
• 0 * 2 hoch 3 = 0
• 1 * 2 hoch 4 = 16
• 0 * 2 hoch 5 = 0
• 0 * 2 hoch 6 = 0
• 0 * 2 hoch 7 = 0
• 1 * 2 hoch 8 = 256

Die Summe aus 256 + 16 + 4 + 1 + 1 ist dann 279.
Die binäre Zahl 100010111 entspricht somit der Dezimalzahl 279.

Was bedeuten demnach die Bits und Bytes in einem Binärsystem?

Im Dezimalsystem findest du ebenfalls Einheiten, wie Millimeter, Zentimeter oder Dezimeter.
Diese lassen sich alle, als 10-er Potenz darstellen.

• Milli von Millimeter bedeutet ein Tausendstel Meter und somit 10 hoch -3.
• Zenti von Zentimeter bedeutet ein Hundertstel Meter und somit 10 hoch -2.
• Dezi von Dezimeter bedeutet ein Zehntel Meter und somit 10 hoch -1.
• Nicht ganz so geläufig aber – Deka von Dekagramm bedeutet Zehnfach und somit 10 hoch 1.
• Hekto von Hektoliter bedeutet Hundertfach und somit 10 hoch 2.
• Kilo von Kilogramm bedeutet Tausendfach und somit 10 hoch 3.
• Mega von Megatonnen bedeutet Millionenfach und somit 10 hoch 6.

Bits und Bytes sind auch nur Einheiten.
Jedoch basieren diese auf die zweier-Potenzen des Dualsystems.

Ein Bit ist die kleinste Einheit.
Es kann genau einen Zustand speichern.

• 0 oder 1
• Wahr oder Falsch
• An oder Aus

Der Datentyp boolean, welchen Java und auch andere Programmiersprachen verwenden – entspricht einem Bit.
In einer Variablen vom Datentyp boolean kann somit genau ein Zustand – wahr oder falsch – gespeichert werden.

Da sich mit so einem Bit noch nicht viel anfangen lässt, fasst man mehrere Bits in einem Byte zusammen.
Und zwar 8.
8 Bits sind ein Byte.

Ein Byte kann insgesamt 256 Zustände speichern.

Die kleinste binäre Zahl ist die 0.
Da ein Byte 8 Bits speichert, kann der Zustand Null – 8 mal auftreten.

In Byteschreibweise wäre demnach der kleinste Zustand dann 8 mal die Null: 00000000.
00000000 wie auch nur eine binäre 0 entspräche der Dezimalzahl 0.

Jetzt sind bei 8-Ziffern aber jede Menge Kombinationen möglich.

Echt?
Schauen wir uns die Kombinationen der ersten drei Stellen einmal an.

1. 00000000
2. 10000000
3. 11000000
4. 11100000
5. 00100000
6. 01000000
7. 01100000
8. 10100000

Du hast bei drei Stellen schon acht Möglichkeiten die 0 und 1 zu kombinieren.
Dies entspricht der Potenz 2³.

Insgesamt ergeben sich:
= 1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20
= 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
=255
Wobei die Null, als Byteschreibweise 00000000, noch nicht enthalten ist.
Es ergeben sich somit 256 Möglichkeiten oder 2 hoch 8 Möglichkeiten.

256 Möglichkeiten sind immer noch nicht genug.
Und deshalb wurden, im Laufe der Zeit, immer größere Zustands-Speicher-Möglichkeiten geschaffen.

Terrabyte, Kilobyte, Megabyte und Gigabyte

• Ein Kilobyte sind ca. tausend Byte. Genauer: 2 hoch 10 Byte = 1.024 Byte
• Ein Megabyte sind ca. eine Millionen Byte. Genauer: 2 hoch 20 Byte = 1.048.576 Byte
• Ein Gigabyte sind ca. eine Milliarde Byte. Genauer: 2 hoch 30 Byte = 1.073.741.824 Byte
• Ein Terrabyte sind ca. eine Billionen Byte, Genauer 2 hoch 40 Byte = 1.099.511.627.776 Byte

Zusammenfassung:

• In der Informatik spielt das Dualsystem eine wichtige Rolle.
• In jedem Binären Zahlensystem existieren immer nur zwei Zahlen.
  Normalerweise verwendet man die Zahlen 0 und 1, da sich mit diesen leichter rechnen lässt.
• 0 und 1 kann dabei jeder Zustand sein: „AN“ und „AUS“ bzw. „TRUE“ und „FALSE“.
• Beim Umrechnen von Binärzahlen in Dezimalzahlen, ersetzt du lediglich die Zehnerpotenz aus dem Dezimalsystem – durch eine Zweierpotenz.
  Die Summe aller Zweierpotenzen ist dann die Dezimalzahl.

Über den Autor

Folge Sciodoo und bleibe stets auf dem Laufenden. Schließ dich uns an und abonniere unseren Instagram-Kanal ein. Wir stellen täglich neue Artikel für dich rein. Weiter zum Kanal>>>